Teoría de la Dualidad y Métodos de Análisis
Es una teoría que surgen como consecuencia de una profundización en el estudio de la Programación Lineal. La idea fundamental de la dualidad en programación lineal es que todo programa lineal llamado primal, lleva asociado un programa simpetrico a él, llamado dual. De manera que al resolver el programa lineal original, se obtiene una solución para su problema dual.
El problema fue propuesto en el siglo XVII por Fermat. Establecía que si tenemos los puntos P1, P2 y P3 en un mismo plano, buscáramos un punto P que minimice la suma de distancias. Es decir, la suma de distancias desde dicho punto P hasta P1, P2 y P3.
El dualismo surge porque la distribución de los recursos y la formación de los precios son dos aspectos del mismo problema.
Importancia
- Permite resolver problemas de PL de manera más rápida y sencilla.
- Es otra vía para resolver un problema de PL.
- Facilita profundizar en el contenido económico del problema primal original.
- Puede ser utilizada para resolver el caso en que se debe considerar la introducción de una nueva variable en el primal una vez que ha sido obtenida la solución óptima.
Aplicaciones del Modelo de Transporte
- Nivel de oferta en cada fuente y la cantidad de demanda en cada destino.
- El costo de transporte unitario de la mercancía a cada destino.
Diremos que Santiago, Concepción y Temuco demandan 250 ton, 100 ton y 50 ton de productos del mar, respectivamente. Quienes van a proveer de los productos son dos empresas que están ubicados en Puerto Montt y Puerto Natales, donde la capacidad de producción es de 150 ton y 250 ton respectivamente (Vamos a suponer, para este ejemplo, que están en equilibrio la oferta y la demanda).
En este problema tenemos que cada nodo representa el origen (i) y el destino (j), tal y como se muestra en la figura. Los arcos son los que unen los orígenes con los destinos. A su vez, tenemos que cada origen transporta una cantidad de carga al destino, denotado como Xij, mientras que los costos por transportar dicha carga del origen al destino se denota cómo Cij. Finalmente, Oi corresponde a la oferta de los orígenes, o dicho de otra forma, las capacidades de producción. Mientras que Dj son la demanda de los destinos. Dicho esto, las denotaciones quedarían de la siguiente forma:
- i:1 = Puerto Montt corresponde al nodo 1 del origen.
- i:2 = Puerto Natales corresponde al nodo 2 del origen.
- j:1 = Santiago corresponde al nodo 1 del destino.
- j:2 = Concepción corresponde al nodo 2 del destino.
- j:3 = Temuco corresponde al nodo 3 del destino.
Por otra parte, la oferta y demanda quedarían definidas de la siguiente forma:
- O1 = 150 ton
- O2 = 250 ton
- D1 = 250 ton
- D2 = 100 ton
- D3 = 50 ton
Finalmente, los costos por kilómetro de transportes viene dado en la siguiente tabla. Como consideración especial y reiterar lo mencionado en la introducción, estos datos son inventados:
Costos (CLP/km) | Santiago | Concepción | Temuco |
|---|---|---|---|
La distancia desde los puntos de orígenes hasta los destinos vienen dado en la siguiente tabla. Estos datos fueron extraídos por Google:
Distancia (km) | Santiago | Concepción | Temuco |
|---|---|---|---|
El costo total de transportar las carga desde los orígenes hasta los destinos vienen dado en la siguiente tabla:
Costos (CLP) | Santiago | Concepción | Temuco |
|---|---|---|---|
Antes de hacer la fórmula de minimización de costos, hay que establecer la denominación de la cantidad de productos a transportar desde los orígenes hasta los destinos, el cual es de la siguiente forma, Xij. Dicha denominaciones aplicadas al ejemplo vienen dados en la siguiente tabla:
Cantidad de productos a transportar (Xij) | Santiago | Concepción | Temuco | Oferta |
|---|---|---|---|---|
La fórmula de minimización de costos quedaría de la siguiente forma:
Min 103.400X11 + 77.520X12 + 28.240X13 + 224.720X21 + 290.436X22 + 12.300 X33
Sujeto a:
- X11 + X21 = 250
- X12 + X22 = 100
- X13 + X23 = 50
- X11 + X12 + X13 = 150
- X21 + X22 + X23 = 250
- Xij>=0, i=1,2, j=1,2,3
Conclusión
Puerto Montt debe transportar 50 toneladas a Santiago, mientras que a Concepción 100 toneladas. Por otra parte, Puerto Natales deberá transportar 200 y 50 toneladas a Santiago y Temuco, respectivamente.
Cantidad de productos a transportar (Xij) | Santiago | Concepción | Temuco | Oferta |
|---|---|---|---|---|
Al transportar las toneladas de productos de mar hasta los destinos (Santiago, Concepción y Temuco), el costo de transporte sería de $53.981.000 en total, que sería el monto óptimo que minimizaría los costos.
La Formulación con Programación Lineal
El planteamiento es como sigue: llamando Xij al flujo de productos del origen i al destino j , cij al costo unitario por tonelada movida, Si a la oferta de producto en el nodo i , Dj a la demanda de productos en el nodo j, y Z al costo total del plan de transporte, entonces para el caso con dos orígenes y tres destinos, el programa lineal es:
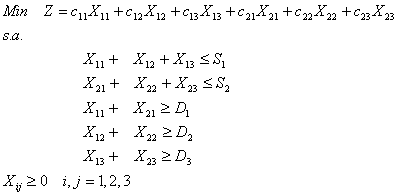…[1]
Éste es el problema del transportista que busca satisfacer la demanda en los destinos a un costo total mínimo. Las restricciones del programa representan la conservación del flujo en los nodos, impidiendo al transportista planear movimientos de carga mayores a la disponibilidad en los orígenes y obligándolo a entregar en los destinos al menos la demanda solicitada
Técnicas y Métodos de Solución para el Problema de Transporte
- 1. En la celda de la esquina Noroeste se debe asignar la máxima cantidad de unidades posibles, cantidad que se ve restringida ya sea por las restricciones de la oferta o de la demanda.
- 2. Se continúa con un barrido fila por fila de izquierda a derecha y de arriba hacia abajo, colocando en cada celda la cantidad que corresponda en función de la disponibilidad y los requerimientos.
- 3. Una vez terminado el proceso iterativo se procede a calcular el costo total de esta solución básica inicial identificando simultáneamente si se trata de una solución degenerada o no degenerada.
- 1. Verificar que oferta y demanda estén en equilibrio. Si no están en equilibrio, se creará un destino o un origen ficticios según corresponda.
- 2. Encontrar la solución básica factible inicial
El proceso se inicia estableciendo la diferencia entre los dos costos más bajos para cada fila y columna. De la totalidad se toma el de mayor valor y esa será la fila o columna a considerar. En función de ello ir asignando volúmenes a transportar comenzando con las celdas de costos más bajos hasta que la oferta o demanda se saturen. De haber valores repetidos, se asigna al azar.
- 3. Determinar si la solución encontrada es degenerada o no, es decir si cumple con la condición de m + n – 1 ≤ #Ca (número de celdas asignadas en solución).
- 4. Convertir la solución degenerada en una no degenerada agregando el número de Ɛ (épsilon) que sean necesarias para hacer cumplir la condición (m+n-1) ≤ Ca
- 5. Determinar los multiplicadores (u y v). El proceso se inicia asumiendo un cero o un 10 a la primera fila o columna (es totalmente arbitrario) para luego ir calculando los valores para cada una de las celdas en solución. Recomendamos asumir u = 0 en la primera fila.
- 1. De la matriz se elige la celda con el menor costo (en caso de haber dos o más celdas con costo igual se elige una en forma arbitraria) y se le asigna la mayor cantidad de unidades posible, cantidad que se ve restringida ya sea por las restricciones de oferta o de demanda. En este mismo paso se procede a ajustar la oferta y demanda de la fila y columna afectada, restándole la cantidad asignada a la celda.
- 2. En cada etapa se asignará la mayor cantidad posible a la celda que le sigue con menor costo y así se prosigue hasta llegar al final de la matriz.
- 3. Se procede al cálculo del costo total.
Comentarios
Publicar un comentario