Modelos Matemáticos de Programación Lineal

 Modelo Matemático de Programación Lineal

      La Programación Lineal (PL) es una de las principales ramas de la IO. En esta categoría se consideran todos aquellos modelos de optimización donde las funciones que lo componen, es decir, función objetivo y restricciones, son funciones lineales en las variables de decisión. 

    Consiste  en una función objetivo y un conjunto de restricciones en la forma de sistema de ecuaciones o inecuaciones. La programación lineal utiliza un modelo matemático para describir el problema. Este modelo está dado por una función lineal de varias variables, en el cual se desean determinar valores no negativos para dichas variables que maximizan o minimizan el valor de la función lineal. Cuando hablamos de programación nos referimos a planeación. 

Elementos

• Variables: simboliza matemáticamente a las variables de decisión.
• Función Objetivo: es la formulación matemática de una meta establecida y por tanto, su valor final mide la efectividad lograda.
• Restricciones: funciones lineales expresadas como igualdades o desigualdades, que limitan el valor de las variables de decisión a valores permisibles. Las restricciones representan recursos, condiciones o requerimientos establecidos. 

Importancia

• Permite la toma de decisiones basada en datos y de manera objetiva. Los modelos matemáticos representan de manera clara la situación a resolver y permiten encontrar la mejor solución.

•  Optimiza procesos y recursos en una gran variedad de campos, tales como: la producción, distribución, planificación y gestión de proyectos, entre otros.  

•  Permite hacer un uso más eficiente de los recursos. 

•  Permite resolver problemas complejos y encontrar soluciones innovadoras, que quizá en otro contexto no se hubiesen imaginado. 

Construcción

    La construcción de modelos matemáticos y la resolución de problemas destacan como componentes de la competencia básica en matemática. 

1. Determinar las variables de decisión y expresarlas algebraicamente.
2. Determinar las restricciones y se expresarlas como ecuaciones o inecuaciones dependientes de las variables de decisión
3. Expresar todas las condiciones implícitamente establecidas por la naturaleza de las variables: que no puedan ser negativas, que sean enteras, que solo puedan tomar determinados valores, ...
4. Determinar la función objetivo.

Modelos Matemáticos

    Trata sobre entender el fenómeno y hacer precciones con respecto a futuros comportamientos. Estos modelos se dividen básicamente en: Modelos Determistas (MD) o Modelos Estocásticos (ME). En el primero (MD) se considera que los parámetros asociados al modelo son conocidos con certeza absoluta, a diferencia de los ME, donde la totalidad o un subconjunto de los parámetros tienen una distribución de probabilidad asociada. 

Método Gráfico

    Este método permite la resolución de problemas sencillos, es útil cuando se trabaja con problemas de programación lineal con sólo dos variables. En este método se grafican las restricciones y la función objetivo en un plano cartesiano y se busca la intersección de las restricciones para encontrar la solución óptima.

1. Se dibuja el sistema de coordenadas asociando a un eje la variable "x" y a otro la "y". 
2. Se marca en dichos ejes una escala numérica apropiada a los valores que pueden tomar las variables de acuerdo a las restricciones del problema. 
3. Se representan las restricciones. 
4. La región factible es la intersección de las regiones delimitadas tanto por el conjunto de restricciones, como por las condiciones de no negatividad de las variables. 

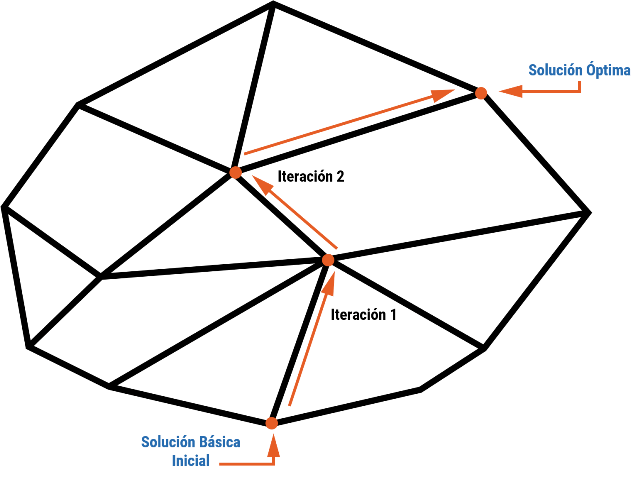
Método Simplex

    Este método fue creado por George Dantzig en 1947, y  es uno de los más utilizados para resolver problemas de programación lineal con varias variables. En este método se construye una tabla que muestra las variables y las restricciones, y se realiza una serie de iteraciones para encontrar la solución óptima. 

    Este método parte de dos afirmaciones importantes, tales como: 

1. El conjunto de posibles soluciones o conjunto factible de cualquier problema puede representarse mediante un poliedro convexo. 
2. Si un problema de programación lineal tiene una solución óptima y finita, esta estará en un vértice del poliedro convexo que representa al problema.

        Tipos de optimización

Objetivo de maximización

Condición de parada: cuando en la fila Z no aparece ningún valor negativo.

Condición de entrada a la base: el menos valor negativo en la fila Z.

Condición de salida de la base: una vez obtenida la variable entrante, la variable que sae se determina mediante el menor cociente. Po/Pj de los estrictamente positivos. 

Objetivo de minimización

Condición de parada: cuando en la fila Z no aparece ningún valor negativo.

Condición de entrada a la base: el mayor valor positivo en la fila Z indica la variable Pj que entra a la base. 

Condición de salida de la base: una vez obtenida la variable entrante, la variable que sae se determina mediante el menor cociente. Po/Pj de los estrictamente negativos. 

Existen casos especiales que se encuentran a menudo en las aplicaciones del método simplex, donde los más importantes son:

• Degeneración: un empate al elegir la variable que sale se rompe arbitrariamente. El problema se conoce como ciclaje. 
• Soluciones óptimas múltiples: problemas que presentan más de una solución óptima. 
• Soluciones óptimas no acotadas: problemas para los cuales una o más de las variables pueden aumentarse indefinidamente mejorando en forma indefinida la función objetivo. 
• Soluciones factibles no existentes: problemas para los cuales no hay espacio de soluciones que cumplan con todas las restricciones.
• Variables no restringidas en signo: existen algunas variables reales que pueden incluir valores negativos.